Definition: Self-inductance is the inherent property of the coil that opposes variation in the current passing through it.
The coil opposes the change of current flowing through it. This property of the coil is called Self-inductance. The opposition offered by a coil depends on the rate of change of the current. The more the rate of change of current, the more the opposition. Why does this opposition to the current take place?
The opposite polarity voltage is induced across the coil, and the magnitude of the voltage induced across the coil depends on the rate of change of current and the self-inductance of the coil. The induced EMF in a coil always opposes the applied voltage.
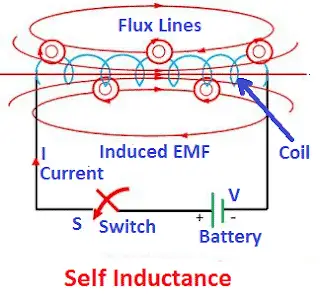
Self-inductance is defined as the induction of voltage in a current-carrying wire when the current in the wire itself changes.
The voltage induced in the current-carrying conductor is;
Thus, the voltage induced in the coil is directly proportional to the number of turns(N) and the rate of change of flux(dΦ/dt). The voltage induced in the coil opposes the applied voltage.
Unit of Self-inductance
The SI unit of inductance is Henry(H), named after Joseph Henry, and its symbol is L. A coil has an inductance of 1 Henry if a current change of 1 ampere per second induces an electromotive force (EMF) of 1 volt in the coil.
1 Henry = 1 Weber per Ampere
Self-inductance Formula
The formula for self-inductance is given by,
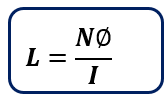
Where:
- L: Inductance (measured in Henries, H)
- N: Number of turns of the coil
- Φ: Magnetic flux linked with the coil (in Webers, Wb)
- I: Current flowing through the coil (in amperes, A)
Derivation of Self-inductance Formula
Faraday’s law of electromagnetic induction is used to derive the formula for the self-inductance of the coil. The voltage induced in a coil depends on the self-inductance of the coil and the rate of change of current in the coil.
Thus, the voltage induced in the coil is,
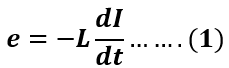
Here, the minus sign shows that the induced voltage opposes the applied voltage.
Therefore, the inductance of the coil is,
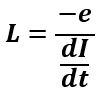
In the above expression, If
e= 1 Volt,
dI/dt = 1 amp/sec,
Then L= 1 Henry
If the voltage induced in the coil is 1 volt when the current flowing through it changes at the rate of 1 Ampere/second, the coil has an inductance of 1 Henry.
Alternatively, the induced voltage in a coil can also be expressed using the inductance (in Henries) and the rate of change of magnetic flux. The induced voltage depends on the rate of change of the flux and the number of turns in a coil.
The induced emf is,
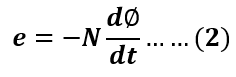
The current is responsible for setting the magnetic flux, therefore the rate of change of flux is caused by the rate of change of current. Hence, the above expression can be rewritten as,
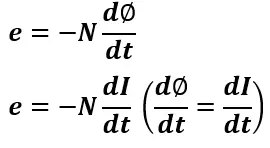
Equating the equations 1 and 2, we get,
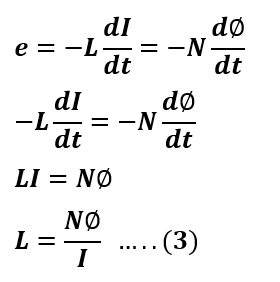
Where,
N = Number of turns
Φ = Flux
I = Current flowing through the coil
Self-inductance of a Solenoid Coil
A solenoid coil is a cylindrical coil of wire that generates a magnetic field when an electric current passes through it. The strength of the magnetic field depends on the number of turns, current, and core material inside the coil. Consider a solenoid with N turns, a length L, and a cross-sectional area A. The current through the solenoid coil is I. The steps for the formula derivation for the solenoid coil are as follows.
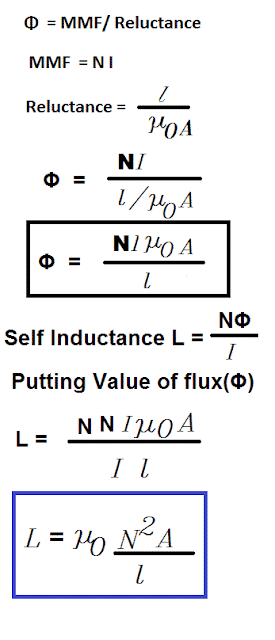
Step 1: Find the MMF( Magnetomotive force)– The MMF is the product of the number of turns and the current flowing in the coil.
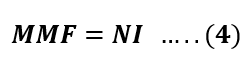
Step 2: Find the Reluctance (S) of the magnetic circuit– The formula for finding magnetic reluctance is,
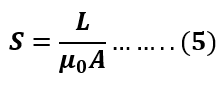
Step 3: Find the Flux
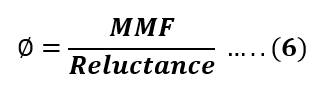
Putting the value of MMF and reluctance from equations 4 and 5 in equation 6, we get,
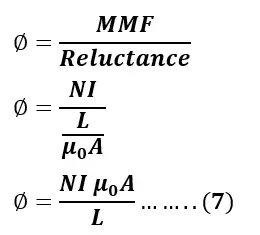
Step 4: Find self-inductance:
Putting the value of flux from equation 7 in the equation 3, we get
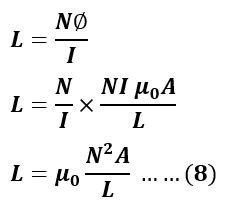
Where, μo is permeability of free space( 4π x 10-7 )
If the core is made of magnetic material of permeability μ, then the equation (8) becomes,
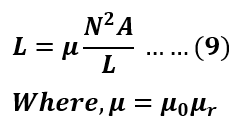
Factors on Which Self-inductance Depends
Self-inductance depends on several key factors that determine the ability of a coil or conductor to oppose changes in current. These factors include:
1. Number of Turns (N): Inductance is directly proportional to the square of the number of turns in the coil. A higher number of turns increases the magnetic flux linkage, resulting in greater inductance.
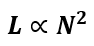
2. Permeability of the core(μ): The type of core material affects inductance significantly. Higher permeability materials (e.g., iron) increase magnetic flux linkage, increasing inductance.
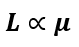
3. Length of the coil(L): Inductance is inversely proportional to the length of the coil. A longer coil reduces the flux density, lowering inductance.
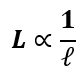
4. Cross-Sectional Area of the Coil (A): Larger cross-sectional areas allow more magnetic flux to pass through, increasing inductance.
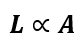
5. Shape and Configuration of the Coil: The geometric arrangement, such as tightly wound coils or spaced windings, affects the concentration of the magnetic field and thus the inductance.
Does Self-inductance Act as an Inertia?
The mechanical equivalent of self-inductance can be understood by comparing it to the inertia of a moving object in mechanics. In both cases, the system resists changes. Self-inductance is the property of a coil or conductor that resists changes in current. It stores energy in the magnetic field created by the current. Inertia is the property of a mass that resists changes in its velocity. It stores energy in the form of kinetic energy when the object is in motion.
Current in a circuit is analogous to velocity in mechanics. Induced EMF is comparable to the force required to change velocity. Inductance (L) is analogous to mass (m) in the mechanical system.
Difference between Mutual-inductance and Self- Inductance
The following are the differences.
| Self-inductance | Mutual-inductance |
| Self-inductance is the opposition to a change in the current caused by induced EMF in a coil. | Mutual inductance is the opposition to a change in current in one coil caused by a change in the current in the nearby second coil |
The formula for self-inductance is.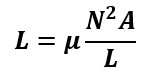 | The formula for the mutual inductance is |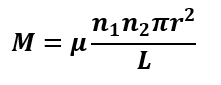
Applications of Self Inductance
1. Inductors in Electrical Circuits: Inductors are widely used in AC and DC circuits for energy storage and current regulation. Inductors oppose changes in current due to the phenomenon of self-inductance.
2. Transformers: Transformers transfer energy between the primary and secondary coils through the principle of self-inductance.
3. Electromagnetic Devices: Self-inductance is important in devices, such as solenoids, relays, and electromagnetic locks. It helps these devices create controlled magnetic fields.
4. Energy Storage: The self-inductance of inductors makes them store energy in their magnetic fields.
5. Tuning Circuits: The inductance property is used in LC (inductor-capacitor) circuits to tune frequencies in radios, oscillators, and signal processing systems.
7. Filters in Communication Systems: The Inductor’s inductive properties are used in low-pass, high-pass, and band-pass filters to shape signal frequencies.
8. Electrical Motors and Generators: The self-inductance of the inductor plays a key role in the functioning of motors and generators as it induces EMF during operation.
9. Surge Protection: Inductors are used to protect electrical systems from voltage spikes by opposing sudden changes in current.
10. Inductive Sensors: The proximity sensor self-inductance property of the inductor to detect position or movement based on magnetic field variations.
Solved Examples
Q1. In a coil, when the current changes from 5 A to 2 A in 0.1 s, the induced EMF is 3 Volts. What is the coil’s inductance?
E=-L(dI/dt)
E=-L[(I2-I1)/(t2-t1)]
3=-L[(2–5)/(0.1–0)]
3= -L(-3/0.1)
3 = 30 L
L= 3/30
L = 0.1 Henry
Q2. What is the self-inductance of a coil when a change of current from 0 to 1A in 0.05s induces an emf of 20 volts?
E=-L(dI/dt)
E=-L[(I2-I1)/(t2-t1)]
20=-L[(0–1)/(0.05–0)]
20= -L(-1/0.05)
20 = 20 L
L= 20/20
L = 1 Henry
Q3.An inductor coil has 400 turns of copper wire, which produce a magnetic flux of 20mWb when a DC current of 10 amperes flows through it. What is the inductance of the coil?
N = 400 Turns
I = 10 Amps.
Φ = 20mWb= 20 x 10-3
= 0.02 Wb
L = N Φ / I
L= 400 x 0.02/ 10
L= 0.8 Henry
Frequently Asked Questions on Self Inductance
Q1. What is self-inductance?
Self-inductance is the property of a coil that opposes the change in the current flowing through it by inducing an electromotive force (EMF) in the same coil.
Q2. What is the SI unit of self-inductance?
The SI unit of self-inductance is the Henry (H).
Q3. How is self-inductance calculated?
Inductance (L) is given by the formula: L=NΦ/I
Where N is the number of turns, Φ is the magnetic flux, and I is the current.
Q4. What factors affect self-inductance?
It depends on:
- Number of turns in the coil (N)
- Area of the coil (A)
- Length of the coil (l)
- Permeability of the core material (μ)
5. Why do inductors oppose changes in current?
Inductors oppose changes in current because of the EMF induced by self-inductance, which resists the variation in the current according to Lenz’s Law.
6. What are the applications of self-inductance?
Self-inductance is used in:
- LC circuits for tuning frequencies
- Motors and generators for energy conversion
- Relays and solenoids for controlled magnetic fields
- Transformers for energy transfer
7. What is the energy stored in an inductor?
The energy stored in an inductor is given by: E=1/2LI2
where L is the inductance and I is the current.
8. Can self-inductance be negative?
No, self-inductance is always positive because it represents the ability of a coil to store energy in a magnetic field.
9. How does self-inductance differ from mutual inductance?
Self-inductance is the EMF induced in a coil by its own changing current, while mutual inductance is the EMF induced in one coil due to the changing current in a neighboring coil.
10. Why is self-inductance important in electrical circuits?
Self-inductance is essential for regulating current flow, energy storage, and the design of components like transformers, inductors, and oscillators.